그래프로 보는 Microservice의 SPOF(Single Point of Failure) 문제 해결과 그 비용

Switch to English

viewof p = Inputs.range([0.01, 0.99], {step: 0.01, value: 0.5, label: "p"});
viewof n = Inputs.range([1, 100], {step: 1, value: 5, label: "n"});

function join(p, n) {
  return Math.pow(p, n);
}
function split(p, m) {
  return 1 - Math.pow(1 - p, m);
}

y1s = (() => {
  const ys = [];
  for (let i = 1; i <= 100; i++) {
    ys.push({
      m: i,
      y: join(split(p, i), n),
      label: "ScaleOutMicroservice",
    });
  }
  return ys;
})();

y2s = (() => {
  const ys = [];
  for (let i = 1; i <= 100; i++) {
    ys.push({
      m: i,
      y: split(join(p, n), i),
      label: "ScaleOutMonolith",
    });
  }
  return ys;
})();

Plot.plot({
  grid: true,
  color: {legend: true, scheme: "BuRd"},
  x: {label: "m"},
  y: {label: "Combined Availability", domain: [0, 1]},
  marks: [
    Plot.areaY(y1s.concat(y2s), {y1: "y", x: "m", fill: "label", fillOpacity: 0.5}),
    Plot.tip(y1s, Plot.pointerX({x: "m", y: "y", fill: "darkgray", title: (d) => `${d.label}(${p}, ${d.m}, ${n})\n${d.y}`})),
    Plot.tip(y2s, Plot.pointerX({x: "m", y: "y", fill: "darkgray", title: (d) => `${d.label}(${p}, ${d.m}, ${n})\n${d.y}`})),
  ],
  style: "background: inherit;",
});

Figure 1: 그래프로 시각화한 수평 확장(Horizontal Scaling, Scale-Out) 시 Microservice의 이점

예시를 통한 Monolith와 Microservice의 비교

소스코드 예시로 이해하는 Monolith와 Microservice의 유사성

웹 개발자 Krtalić Rusendić (2022) 에 따르면, 프로그램 하나를 개발하면 Monolith(Monolithic Architecture), 여러 프로그램으로 구현하면 MSA(Microservice Architecture)이다.

Monolith 프로그램을 구성하는 것은 Class와 Method, 또는 Module과 Function이다 (Krtalić Rusendić 2022). Class와 Method를 Microservice 프로그램으로 구현하면 Service와 API이다 (Krtalić Rusendić 2022). Netflix가 Microservice로 유명하며, Chaos Monkey라는 Test 도구도 개발했다 (Krtalić Rusendić 2022).

Krtalić Rusendić (2022) 는 Monolith와 Microservice의 차이를 알기 쉽게 시각화한다. 그러나 Krtalić Rusendić (2022) 가 제시한 예시 프로그램의 가용성이 Monolith로 구현하면 \(50\%\), Microservice는 \(25\%\)라는 그의 주장은 설득력이 떨어진다. 소스코드 내 결함으로 인한 장애는, Monolith 프로그램 1개로 배포하든 Microservice 프로그램 2개로 배포하든 배포 방식과는 무관하게 \(25\%\)가 되어야 한다. 예를 들어 0과 1을 랜덤하게 2번 뽑아 합이 0일 때만 출력하는 소스코드를 실행할 때, 장애가 발생하지 않는다면 랜덤 생성 과정이 순차적이든 병렬적이든 배포 형태가 Monolith이든 Microservice이든 출력의 가용성은 \(25\%\)로 같다. 이 프로그램에서 출력의 SPOF(Single Point of Failure)는 Microservice로 배포할 때 2개로 늘어나는 것이 아니고, 결과 간의 의존성 때문에 Monolith로 배포해도 소스코드 내에서 2개이다.

소스코드 예시로 이해하는 Microservice의 부분적 이점

Microservice로 설계하고 나면 배포 방식이 Microservice가 아니라 Monolith로 배포하더라도 유리할 수 있다. 앞서 언급한 소스코드에서 두 결과의 합만을 출력할 것이 아니라, 첫 번째 결과가 0인 경우 두 번째 결과에 의존하지 않고 부분적으로라도 결과를 출력하는 기능을 추가한다면 그 가용성은 \(50\%\)이다. 이 출력의 SPOF(Single Point of Failure)는 첫 번째 결과 1개이면 되는데 괜히 두 번째 결과까지 포함해서 2개로 늘리고 가용성을 \(25\%\)로 줄일 필요가 없다. 이처럼 부분 가용성(Resilience)은 Microservice를 감안해서 설계해야, Monolith로 배포하더라도 SPOF(Single Point of Failure)를 불필요하게 늘리지 않을 수 있다.

낸드플래시(NAND Flash) 반도체 메모리로 이해하는 Monolith와 Microservice 간 기회비용

소스코드 외적으로, Monolith 대비 Microservice의 비용이 있는 것은 사실이다 (see Krtalić Rusendić 2022). 예시 소스코드 2개가 의존하는 하드웨어가 1개일 때 소스코드 외적인 가용성이 \(50\%\)라면, 소스코드 1개에 하드웨어 1개씩 총 2개의 하드웨어에 의존할 때 가용성은 하드웨어의 개별적인 동작 때문에 \(25\%\)로 줄어든다고 볼 수도 있다.

그러나 Microservice 대비 Monolith의 비용도 간과해서는 안 된다. 2개의 소스코드가 하드웨어 1개씩 총 2개에 의존할 때 소스코드 외적인 가용성이 \(25\%\)였다면, 이번에는 역으로 다시 총 1개의 하드웨어에 의존할 때 가용성은 한정된 자원에 대한 경합(Contention) 때문에 \(12.5\%\)로 더 줄어들 위험도 있다. 예를 들어 낸드플래시(NAND Flash) 반도체 메모리도 마찬가지로 SLC(Single Level Cell), MLC(Multi Level Cell), TLC(Triple Level Cell), QLC(Quadruple Level Cell)의 품질, 즉 성능, 내구성, 신뢰성 등에 마찬가지의 기회비용이 있다고 볼 수 있다 (see Lee 2018). 일반적으로 SLC(Single Level Cell)가 QLC(Quadruple Level Cell)보다 비싸고 좋다. 즉 Monolith가 오히려 QLC(Quadruple Level Cell) 같은 단점이 있다.

이하 내용에서는 소스코드 내적인 관점에서만 가용성을 비교한다.

그림과 함께 이해하는 수평 확장(Horizontal Scaling, Scale-Out) 시 Microservice의 이점

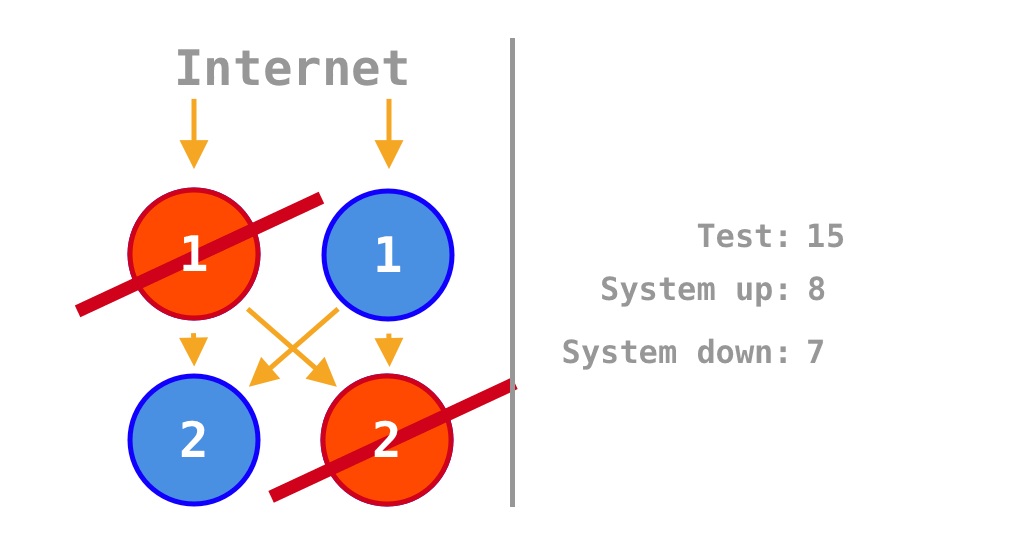
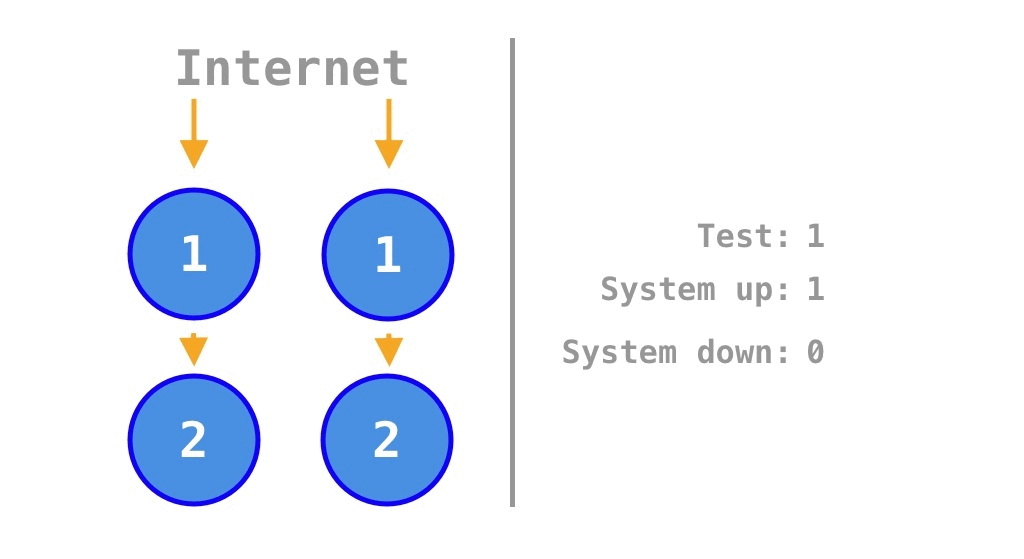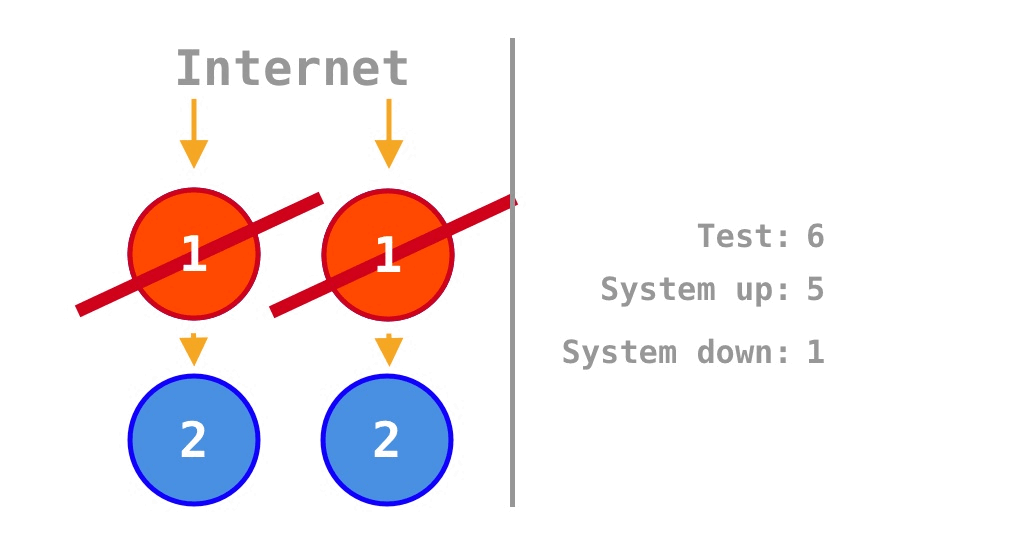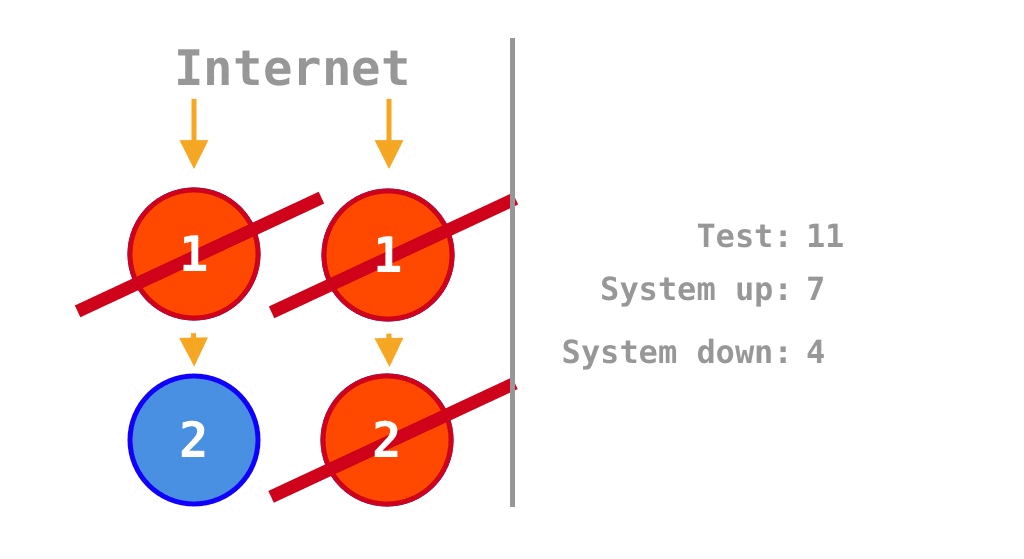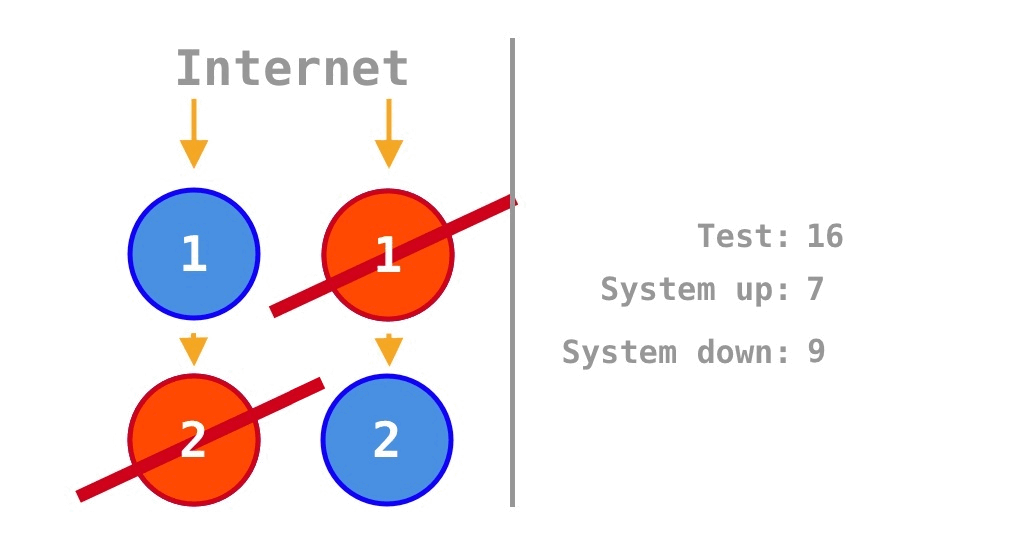
수평 확장(Horizontal Scaling, Scale-Out)은 SPOF(Single Point of Failure)를 제거해 가용성을 확대할 수 있는 전략이다. Krtalić Rusendić (2022) 의 설명을 보면, Figure 2 과 같은 Microservice의 2가지 정상 동작 상태를 16가지 중에서 누락해 가용성을 \(\frac 7 {14} = 50\%\)로 계산하는 사소한 실수가 있었고, Monolith의 가용성 \(75\%\)도 소스코드 내 의존성을 고려하면 더 정확하게 이해할 수 있다.

Figure 2: 수평 확장(Horizontal Scaling, Scale-Out) 시 Microservice의 16가지 상태 중 Krtalić Rusendić (2022) 가 누락한 2가지 정상 동작 상태

예시 소스코드의 2가지 동작 여부에 따라 총 4가지 상태를 탐색하고 가용성 \(\frac 1 4 = 25\%\)를 계산한 것처럼

\[2^2 = 4\]

이므로, 4개의 소스코드 동작 여부에 따라서는, Krtalić Rusendić (2022) 가 정리한 14가지가 아니라 누락된 다음 2가지 상태를 더해 총 16가지 상태를 탐색해야 한다:

\[2^4 = 16.\]

2개의 소스코드를 각각 2배로 늘리면 기존에 2개였던 SPOF(Single Point of Failure)가 제거되어, 가용성은 기존 소스코드 2개의 \(\frac 1 4 = 25\%\)에서

\[\frac 9 {16} = 56.25\%\]

으로 증가한다. \(\frac 9 {16} = 56.25\%\)는 Krtalić Rusendić (2022) 가 계산한 \(\frac 7 {14} = 50\%\)와는 다소 차이가 있다.

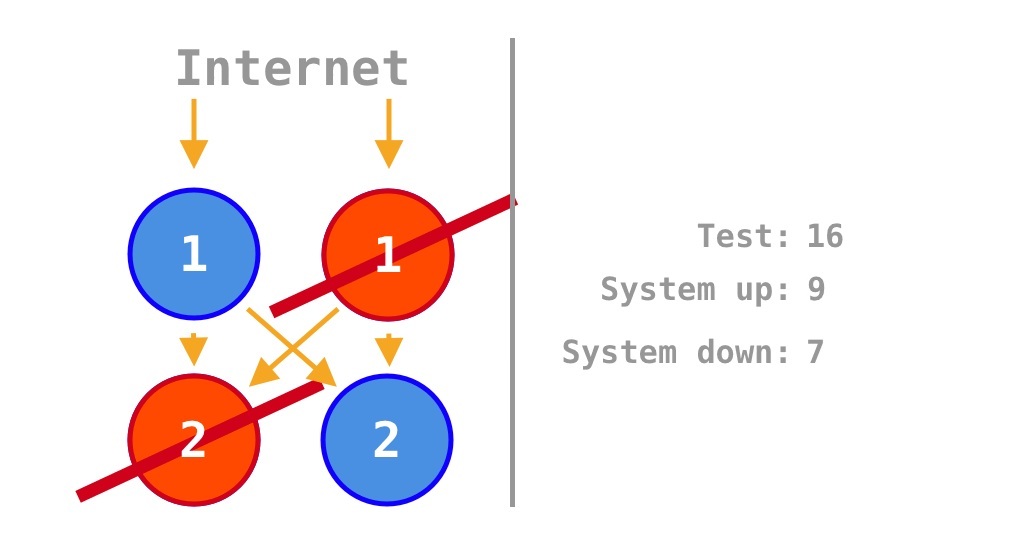
반면 Monolith 프로그램 1개의 SPOF(Single Point of Failure)를 제거하기 위해 기존 프로그램 1개를 2배로 늘리면 프로그램 1개 내부의 소스코드 2개 사이의 의존성은 유지되지만 프로그램 2개 사이의 외부 의존성은 없다. 그래서 Figure 2 의 중앙에 보이던 노란 화살표 2개가 Figure 3 에는 없다. 그러면 Figure 2 의 2가지 정상 동작 상태가 Figure 3 에서 반대로 장애 상태가 되어, 가용성은 프로그램 1개의 \(\frac 1 4 = 25\%\)에서

Figure 3: 수평 확장(Horizontal Scaling, Scale-Out) 시 Monolith의 16가지 상태

\[\frac 7 {16} = 43.75\%\]

으로 증가한다. \(\frac 7 {16} = 43.75\%\)는 Krtalić Rusendić (2022) 가 계산한 \(\frac 3 4 = 75\%\)와는 다소 차이가 있다. 왜냐하면 프로그램 1개에서 4배인 4개로 늘리지 말고 2배로 늘려야 그림처럼 소스코드 내 의존성을 고려한 엄밀한 비교가 가능하기 때문이다.

정리하면 소스코드 내적인 관점에서는 수평 확장(Horizontal Scaling, Scale-Out)한 Monolith의 가용성 \(43.75\%\)가 기존의 \(25\%\)보다 나아지기는 해도 수평 확장(Horizontal Scaling, Scale-Out)한 Microservice의 가용성 \(56.25\%\)보다 오히려 더 못하다는 사실이 Krtalić Rusendić (2022) 의 해석과 다른 점이다.

수식을 통한 Monolith와 Microservice의 비교

소스코드의 관점에서 수식으로 표현한 Monolith와 Microservice의 유사성

일반적으로 소스코드 외적인 요인이 없을 때 \(0 \leq p \leq 1\)의 가용성을 독립적으로 갖는 Microservice \(n\)개가 서로 Fully Connected되어 의존하는 결과는 \(n\)개의 SPOF(Single Point of Failure)를 갖기 때문에 그 가용성은 Microservice로 배포하거나 Monolith로 배포하거나

\[\text{Join}(p, n) = p^n \tag{1}\]

으로 동일하다. \(0 \leq p \leq 1\)이므로 \(n\)이 커질수록 단조적으로 감소(Monotonically Decreasing)한다.

반면에 서로 의존하지 않는 \(m\)개는 SPOF(Single Point of Failure)가 없고 그 가용성은 Microservice로 배포하거나 Monolith로 배포하거나

\[\text{Split}(p, m) = 1 - (1 - p)^m \tag{2}\]

으로 동일하다. 반대로 \(m\)이 커지면 단조적으로 증가(Monotonically Increasing)한다. 왜냐하면 \(0 \leq 1 - p \leq 1\)에서 \((1- p)^m\)이 단조적으로 감소(Monotonically Decreasing)하기 때문이다.

수식으로 표현한 수평 확장(Horizontal Scaling, Scale-Out) 시 Microservice의 결합 가용성

소스코드 외적인 요인이 없을 때 \(0 \leq p \leq 1\)의 가용성을 독립적으로 갖는 Microservice \(n\)개 각각을 \(m\)배 수평 확장(Horizontal Scaling, Scale-Out)하면 각 \(m\)개는 서로 의존하지 않아 SPOF(Single Point of Failure)를 제거하므로 그 가용성은 \(\text{Split}(p, m) = 1 - (1 - p)^m\)이다. \(m\)개씩의 \(n\)개가 서로 Fully Connected되어 \(n\)개의 SPOF(Single Point of Failure)로서 의존하는 결과의 가용성은

\[ \begin{align} \text{ScaleOut}_{\text{Microservice}}(p, n, m) & = \text{Join}(\text{Split}(p, m), n)\\ & = \text{Join}(1 - (1 - p)^m, n)\\ & = (1 - (1 - p)^m)^n \end{align} \tag{3}\]

이다.

Figure 2 의 가용성과 일치함을 알 수 있다:

\[ \begin{align} \text{ScaleOut}_{\text{Microservice}}(\frac 1 2, 2, 2) & = \text{Join}(\text{Split}(\frac 1 2, 2), 2)\\ & = \text{Join}(1 - (1 - \frac 1 2)^2, 2)\\ & = \text{Join}(1 - (\frac 1 2)^2, 2)\\ & = \text{Join}(1 - \frac 1 4, 2)\\ & = \text{Join}(\frac 3 4, 2)\\ & = (\frac 3 4)^2\\ & = \frac 9 {16}\\ & = 56.25\%. \end{align} \]

수식으로 표현한 수평 확장(Horizontal Scaling, Scale-Out) 시 Monolith의 결합 가용성

소스코드 외적인 요인이 없을 때 \(0 \leq p \leq 1\)의 가용성을 독립적으로 갖고 서로 Fully Connected되어 \(n\)개의 SPOF(Single Point of Failure)로서 의존하는 Microservice \(n\)개를 Monolith로 배포하면 그 결과의 가용성은 \(\text{Join}(p, n) = p^n\)이다. \(n\)개를 서로 의존하지 않게 \(m\)배 수평 확장(Horizontal Scaling, Scale-Out)하면 SPOF(Single Point of Failure)를 제거하므로 그 가용성은

\[ \begin{align} \text{ScaleOut}_{\text{Monolith}}(p, n, m) & = \text{Split}(\text{Join}(p, n), m)\\ & = \text{Split}(p^n, m)\\ & = 1 - (1 - p^n)^m \end{align} \tag{4}\]

이다.

Figure 3 의 가용성과 일치함을 알 수 있다:

\[ \begin{align} \text{ScaleOut}_{\text{Monolith}}(\frac 1 2, 2, 2) & = \text{Split}(\text{Join}(\frac 1 2, 2), 2)\\ & = \text{Split}((\frac 1 2)^2, 2)\\ & = \text{Split}(\frac 1 4, 2)\\ & = 1 - (1 - \frac 1 4)^2\\ & = 1 - (\frac 3 4)^2\\ & = 1 - \frac 9 {16}\\ & = \frac 7 {16}\\ & = 43.75\%. \end{align} \]

수식으로 정리한 수평 확장(Horizontal Scaling, Scale-Out) 시 Microservice의 이점

다음을 증명할 수 있다 (Sil 2016):

\[(1 - (1 - p)^m)^n + (1 - p^n)^m \geq 1. \tag{5}\]

따라서,

\[ \begin{align} (1 - (1 - p)^m)^n & \geq 1 - (1 - p^n)^m\\ \text{Join}(\text{Split}(p, m), n) & \geq \text{Split}(\text{Join}(p, n), m)\\ \\ \therefore \text{ScaleOut}_{\text{Microservice}}(p, n, m) & \geq \text{ScaleOut}_{\text{Monolith}}(p, n, m). \end{align} \tag{6}\]

그래프로 시각화한 수평 확장(Horizontal Scaling, Scale-Out) 시 Microservice의 이점

Equation 6 의 성질뿐 아니라 Figure 1 의 시각화를 통해 \(\text{ScaleOut}_{\text{Microservice}}(p, n, m)\)과 \(\text{ScaleOut}_{\text{Monolith}}(p, n, m)\)의 격차가 수평 확장(Horizontal Scaling, Scale-Out)의 배수 \(m\)의 확대에도 불구하고 \(p\)의 감소 또는 \(n\)의 증가에 따라 급격히 커진다는 성질도 확인할 수 있다.

결론

결론적으로 소스코드 외적인 요인이 없을 때 \(m\)배의 일괄적인 수평 확장(Horizontal Scaling, Scale-Out)을 시도하면 Microservice를 통해 SPOF(Single Point of Failure)를 내부적으로 제거하는 것이 Monolith를 통해 외부적으로 제거하는 것보다 결합적인 가용성이 더 좋다. 이때 미리 Microservice로 설계하는 경우 나중에 Monolith로 배포하더라도 부분적인 가용성을 제공할 수 있다는 이점도 있다. 다만 소스코드 외적으로는 Monolith 배포에서 한정된 자원에 대한 경합(Contention) 문제와 Microservice 배포에서 다양한 자원에 대한 의존성이 늘어나는 문제를 둘다 감안해야 한다.

References

Krtalić Rusendić, Stanko. 2022. “"Having a Monolith Is a Single Point of Failure".” September 30, 2022. https://stanko.io/having-a-monolith-is-a-single-point-of-failure-3cYdY3KZ7qHW.

Lee, Heeyeol. 2018. “[궁금한 반도체 WHY] 낸드플래시 메모리의 데이터 저장방식, 어떻게 다를까? SLC/MLC/TLC/QLC.” December 26, 2018. https://news.skhynix.co.kr/data-in-nand-flash-memory/.

Sil. 2016. “If \(p + q = 1\) Prove That for Any Natural \(n, m\) Following Is True: \((1 - p^n)^m + (1 - q^m)^n \ge 1\).” December 8, 2016. https://math.stackexchange.com/a/2049972.